
Visualize the quantiles of exponential Distribution $$ \begin$ percentile of given Exponential distribution is 1.3862944. Then the probability distribution of $X$ is It is routinely used as a survival distribution in survival analysis and reliability analysis. Exponential DistributionĮxponential distribution distribution is a continuous type probability distribution.Įxponential distribution is often used to model the lifetime of electric components.
#Cdf exponential distribution how to#
In this tutorial, you will learn about how to use dexp(), pexp(), qexp() and rexp() functions in R programming language to compute the individual probabilities, cumulative probabilities, quantiles and to generate random sample for Exponential distribution.īefore we discuss R functions for Exponential distribution, let us see what is Exponential distribution.

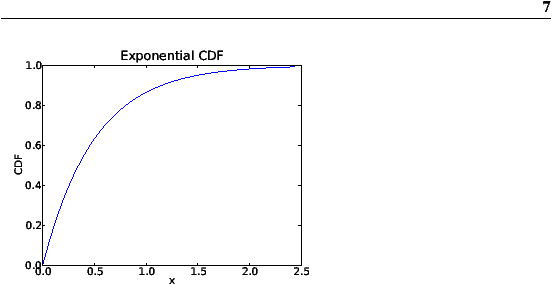
1 Exponential Distribution probabilities using R.This example comes from Ross (2006, Fourth Edition). (Of course, the simpler way is to use x = RAND("Expo")!) The UNIVARIATE procedure is used to check that the data follow an exponential distribution. The following DATA step generates random values from the exponential distribution by generating random uniform values from U(0,1) and applying the inverse CDF of the exponential distribution. This function can be explicitly inverted by solving for x in the equation F(x) = u. The exponential distribution has probability density f(x) = e –x, x ≥ 0, and therefore the cumulative distribution is the integral of the density: F(x) = 1 – e –x. To illustrate the inverse CDF sampling technique (also called the inverse transformation algorithm), consider sampling from a standard exponential distribution. This article is taken from Chapter 7 of my book Simulating Data with SAS. Therefore, if U is a uniform random variable on (0,1), then X = F –1(U) has the distribution F. The inverse CDF technique for generating a random sample uses the fact that a continuous CDF, F, is a one-to-one mapping of the domain of the CDF into the interval (0,1). If you know the cumulative distribution function (CDF) of a probability distribution, then you can always generate a random sample from that distribution. However, one technique stands out because of its generality and simplicity: the inverse CDF sampling technique. There are many techniques for generating random variates from a specified probability distribution such as the normal, exponential, or gamma distribution.


 0 kommentar(er)
0 kommentar(er)
